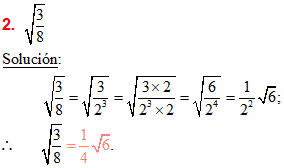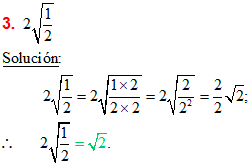Procedimiento 1.  Se factoriza el subradical: de los radicales solo se pueden sacar factores. 2.  La parte numérica se descompone en factores de tal forma que los más sean     potencias con exponentes múltiplos del índice de la raíz: para luego poder sacar del radical dichas potencias al dividir el exponente por el índice 3.  La parte literal se descompone de tal manera que se exprese la mayor parte posible con exponentes múltiplos del índice de la raíz 4.  Se multiplica tanto el numerador como el denominador por la cantidad necesaria que haga que el denominador tenga raíz exacta